Question

The angle of elevation of the top of a tower from a point on the ground is 50 degrees. After moving 50 meters away from the tower, the angle of elevation reduced to 40 degrees. Find the height of the tower?

Answer 1

The height of the tower is 141.74 meters.

Explanation:

See the attached diagram.

Let the position of the tower os AB with A as the base and B is the top.

Now, angle of elevation of point B from point C is 50°, and the from point D is 40°, and hence, CD = 50 meters,

Now, from Δ ABC,
`\tan 50 = (AB)/(AC) = (x)/(AC)`

⇒
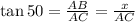
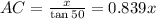`AC = (x)/(\tan 50) = 0.839x` .......... (1)

Again, from Δ ABD,
`\tan 40 = (AB)/(AD) = (x)/(AD)`

⇒
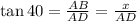
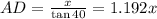`AD = (x)/(\tan 40) =1.192x` .......... (2)

Now, DC = AD - AC

⇒ 50 = 1.192x - 0.839x

⇒ 50 = 0.353x

⇒ x = 141.74 meters.

Hence, the height of the tower is 141.74 meters. (Answer)