Question

At the high school championship game, the Cougars beat the Lions 31 to 17. The total score came from 14 scoring plays. The scoring plays consisted of touchdowns, extra-point kicks, and field goals. Touchdowns are worth 6 points each, extra-point kicks are worth 1 point each, and field goals are worth 3 points each. The number of touchdowns was equal to the number of extra-point kicks. Write a linear system to represent this game. Use matrices to then solve the system. How many touchdowns, extra-point kicks, and field goals occurred in the game?

Answer 1

Number of touchdowns = 2

Number of extra points = 2

Number of field goals = 0

Explanation:

Let the number of touchdowns be "x", number of extra points be "y" and number of field goals be "z".

It is given that number of touchdowns = number of extra points.

Thus, x=y

Total points scored are 14.

Points scored by touch down are = (6)(x)

Points scored by extra points are = (1)(y) = x

Points scored by field goals are = (3)(z)

Thus, the equation becomes

`6x+y+3z = 6x+x+3z=7x+3z = 14`

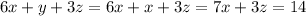
In matrice form, they can be represented as;

`\left[\begin{array}{ccc}6&1&3\end{array}\right] \left[\begin{array}{ccc}x\\y\\z\end{array}\right] = \left[\begin{array}{ccc}1&0&0\\0&1&0\\0&0&1\end{array}\right] (14)`

`x= (14-3z)/(7)`

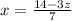
now, x and z cannot be negative or fraction, only positive integers. Thus inserting values of z from 0 to 4,

The correct solution is x=y=2 and z=0.