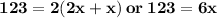Question

Write an equation for the description.

The length of a rectangle is twice its width. The perimeter of the rectangle is 123 feet.

Answer 1

The equation for the description is:
`\mathbf{123=2(2x+x)\:or\:123=6x}`

Explanation:

We need to write an equation for the description.

The length of a rectangle is twice its width. The perimeter of the rectangle is 123 feet.

Let Width of rectangle = x

Length of rectangle = 2x (twice its width means, multiplying 2 with width)

Perimeter of rectangle = 123 feet

The formula used is:
`Perimeter\:of\:rectangle=2(Length* Width)`

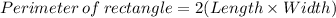
Putting values and finding equation:

`Perimeter\:of\:rectangle=2(Length+ Width)\\123=2(2x+x)`

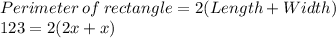
So, the equation for the description is:
`\mathbf{123=2(2x+x)}`

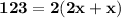
You can simplify the equation as:

`123=2(2x+x)\\123=2(3x)\\123=6x`

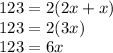
Both equations can be used:
`\mathbf{123=2(2x+x)\:or\:123=6x}`