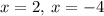Question

Drag numbers to the lines to show the zeros of the function f(x)=x{2}+2x-8

Answer 1

The zeros of the function:

`x=2,\:x=-4`

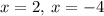
Explanation:

Given the function

`f\left(x\right)=x^2+2x-8`

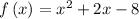
In order to determine the zeros of the function, substitute f(x) = 0

`x^2+2x-8\:=0`

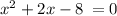
Breaking the expression x²+2x-8=0 into groups

`\:\left(x^2-2x\right)+\left(4x-8\right)=0`

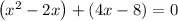
Factor out x from x²-2x: x(x-2)

Factor out 4 from 4x-8: 4(x-2)

so

`x\left(x-2\right)+4\left(x-2\right)=0`

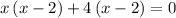
Factor out common term: x-2

`\left(x-2\right)\left(x+4\right)=0`

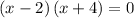
Using the zero factor principle

if ab=0, then a=0 or b=0 (or both a=0 and b=0)

`x-2=0\quad \mathrm{or}\quad \:x+4=0`

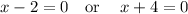
solving x+2 = 0

x+2 = 0

x = -2

solving x+4=0

x+4 = 0

x = -4

Therefore, the zeros of the function:

`x=2,\:x=-4`