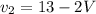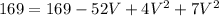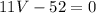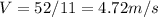Answer:
4.72 m/s
Step-by-step explanation:
Since the collision is perfectly elastic, both momentum and energy is conserved
Momenum:
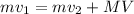
Kinetic energy:
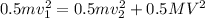
where m = 3.5 kg is the mass of the small moving object at speed v1 = 13 m/s. M = 7 kg is the mass of the big collided object with speed V post-collision. v2 is the speed of the small object post-collision.
Momentum:
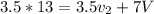
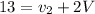
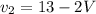
Energy:
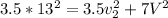
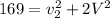
We can substitute