To solve this problem we need to use the proportional relationships between density, mass and volume, together with Newton's second law.
The force can be described as
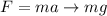
Where,
m = Mass
g = Gravitational acceleration
At the same time the Density can be defined as
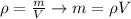
Where,
m = mass
V = Volume
Replacing the value of the mass at the equation of Force we have,
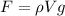
Since the difference between the two forces gives us the total Force then we have to
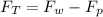
Where
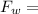 Force of the water
Force of the water
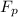 = Force of plastic
= Force of plastic
Therefore with the values for this force we have,

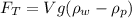
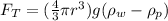
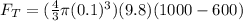
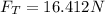
Therefore the tension in the thread is 16.412N