Answer:
Speed of the truck should be 64.03 miles per hour to minimize the cost.
Step-by-step explanation:
Data provided in the question:
Distance = 150 miles
Wage = $14 per hour
Cost of fuel = ( v² ÷ 250 )
Now,
Total time taken = Distance ÷ speed
= 150 ÷ v
Therefore,
Total cost, TC = Wage + Cost of fuel
= $14 × (150 ÷ v) + ( v² ÷ 250 )
=
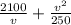
for point of minima differentiating with respect to 'v'
TC'(v) =
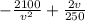 = 0
= 0
or
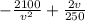 = 0
= 0
or
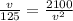
or
v³ = 2100 × 125
or
v = ∛262500
or
v = 64.03 miles per hour
hence,
Speed of the truck should be 64.03 miles per hour to minimize the cost.