Question

A report states that the mean yearly salary offer for students graduating with a degree in accounting is $48,733. Suppose that a random sample of 50 accounting graduates at a large university who received job offers resulted in a mean offer of $49,830 and a standard deviation of $3700. Do the sample data provide strong support for the claim that the mean salary offer for accounting graduates of this university is higher than the national average of $48,733? Test the relevant hypotheses usingα = 0.05.(Use a statistical computer package to calculate the P-value. Round your test statistic to two decimal places and your P-value to three decimal places.)t = P-value = State your conclusion.a. Reject H0. We have convincing evidence that the mean salary offer for accounting graduates of this university is higher than the national average of $48,733.b. Do not reject H0. We do not have convincing evidence that the mean salary offer for accounting graduates of this university is higher than the national average of $48,733. c. Do not reject H0. We have convincing evidence that the mean salary offer for accounting graduates of this university is higher than the national average of $48,733.d. Reject H0. We do not have convincing evidence that the mean salary offer for accounting graduates of this university is higher than the national average of $48,733.

Answer 1

Answer: d

Explanation:

A statistical test for this situation would be of the form:

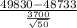`(49830-48733)/((3700)/(√(50) ) )` (49830-48733 ÷ standard error)

(standard error = standard deviation ÷√sample size)

The t-test value obtained is [49830-48733 ÷ (3700÷√50)] = 2.096...

At α = 0.05 this gives a critical value of 1.96 which is smaller than the test statistic obtained above. Therefore we reject the null hypothesis that mean salary offer for accounting graduates of this university is higher than the national average of $48,733