Answer:
The ball is at a height of 120ft when t = 2.2 and when t = 3.5.
Explanation:
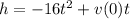
A ball is thrown vertically in the air with a velocity of 90ft/s.
This means that v(0) = 90. So
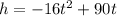
Use the projectile formula h=−16t2+v0t to determine at what time(s), in seconds, the ball is at a height of 120ft.
This is t when
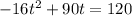
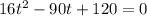
Finding t
Given a second order polynomial expressed by the following equation:
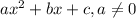 .
.
This polynomial has roots
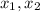 such that
such that
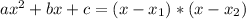 , given by the following formulas:
, given by the following formulas:
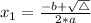
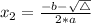
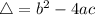
In this problem:
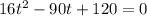
So
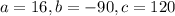
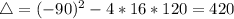
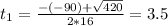
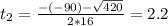
The ball is at a height of 120ft when t = 2.2 and when t = 3.5.