Answer:
Induced current,

Step-by-step explanation:
Given that,
Area of cross section of the wire,
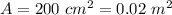
Time, t = 2.2 s
Initial magnetic field,
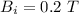
Final magnetic field,
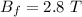
Resistance of the coil, R = 8 ohms
The expression for the induced emf is given by :
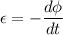
 = magnetic flux
= magnetic flux
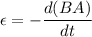

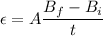
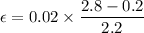
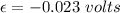
So, the induced emf in the loop is 0.023 volts. The induced current can be calculated using Ohm's law as :
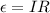

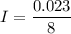

So, the magnitude of the induced current in the loop of wire is
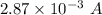 . Hence, this is the required solution.
. Hence, this is the required solution.