1 Answer

Zin Win Htet · Answer 1 · 2020-04-14T05:17:02+0000

Answer:

The dimensions of the barrel that makes minimum its cost of construction are

radius = 3 feet, height = 12 feet.

Explanation:

Let r and h be the radius and height of the cylinder respectively.

Let s be the cost per square foot of the material used to construct the sides of the barrel.

The surface of the sides is the height times the perimeter of the top (or bottom) circumference:

h2πr

hence the cost to make the sides is

h2πrs

The surface of the top and bottom is two times the surface of the circumferences

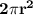
$\bf 2\pi r^2$

Since the cost of the material to make the top and bottom costs double than the material for the sides, the cost to make the top and bottom is

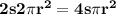
$\bf 2s2\pi r^2 =4s\pi r^2$

The total cost to construct the barrel is then

$\bf C=h2\pi rs+4s\pi r^2$

We have that the volume of the barrel is 108π, so

$\bf \pi r^2h=108\pi$

and

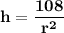
$\bf h=\displaystyle(108)/(r^2)$

replacing this expression in the formula for the cost:

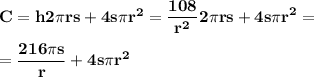
$\bf C=h2\pi rs+4s\pi r^2=\displaystyle(108)/(r^2)2\pi rs+4s\pi r^2=\\\\=\displaystyle(216\pi s)/(r)+4s\pi r^2$

Taking the derivative with respect to r:

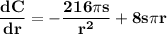
$\bf \displaystyle(dC)/(dr)=-\displaystyle(216\pi s)/(r^2)+8s\pi r$

The critical points are the points where the derivative vanishes

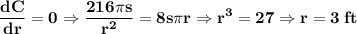
$\bf \displaystyle(dC)/(dr)=0\Rightarrow \displaystyle(216\pi s)/(r^2)=8s\pi r\Rightarrow r^3=27\Rightarrow r=3\;ft$

So r = 3 is a critical point. Taking the second derivative and evaluating it in r=3 we can see it is greater than zero so r = 3 is a minimum:

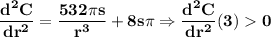
$\bf \displaystyle(d^2C)/(dr^2)=(532\pi s)/(r^3)+8s\pi\Rightarrow (d^2C)/(dr^2)(3)>0$

If r=3 ft. then h=12 ft.

We conclude that the dimensions of the barrel that makes minimum its cost of construction are:

radius = 3 feet, height = 12 feet.

Please log in or register to add a comment.