Question

A certain tuning fork vibrates at a frequency of 215 Hz while each tip of its two prongs has an amplitude of 0.832 mm. (a) What is the period of this motion? ms (b) Find the wavelength of the sound produced by the vibrating fork, taking the speed of sound in air to be 343 m/s.

Answer 1

Step-by-step explanation:

It is given that,

Frequency of vibration, f = 215 Hz

Amplitude, A = 0.832 mm

(a) Let T is the period of this motion. It is given by the following relation as :

`T=(1)/(f)`

`T=(1)/(215)`

`T=4.65* 10^(-3)\ s`

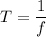
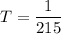
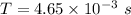
(b) Speed of sound in air, v = 343 m/s

It can be given by :

`v=f* \lambda`

`\lambda=(v)/(f)`

`\lambda=(343\ m/s)/(215\ Hz)`

`\lambda=1.59\ m`

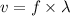
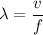
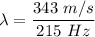
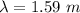
Hence, this is the required solution.