Question

Kenji has at most $30 to spend on lily bulbs and tulip bulbs at his local flower store. Lily bulbs cost $4 each, and tulip bulbs cost $2 each. Tax is included in the prices of the bulbs.

Create a constraint that can be used to represent all possible numbers of lily bulbs, x, and tulip bulbs, y, Kenji can buy

Answer 1

`\left\{\begin{array}{l}x\ge 0\\ \\y\ge 0\\ \\2x+y\le 15\end{array}\right.`

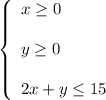
Explanation:

Let x be the number of lily bulbs and y be the number of tulip bulbs Kenji bought. Note that
`x\ge 0, \ y\ge 0.`

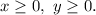
Lily bulbs cost $4 each, then x lily bulbs cost $4x.

Tulip bulbs cost $2 each, then y tulip bulbs cost $2y.

In total, x lily bulbs and y tulip bulbs cost
`\$(4x+2y).`

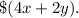
Kenji has at most $30 to spend on lily bulbs and tulip bulbs at his local flower store, so

`4x+2y\le 30\\ \\2x+y\le 15`

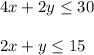
So, you get the system of three inequalities:

`\left\{\begin{array}{l}x\ge 0\\ \\y\ge 0\\ \\2x+y\le 15\end{array}\right.`

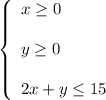
Attached diagram shows the solution set - triangle with verticis (0,0), (0,15) and (7.5,0). All points inside this triangle are the solutions (possible numbers of lily bulbs, x, and tulip bulbs, y).