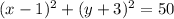Question

Find an equation of the circle that has center , 1−3 and passes through , −6−2.

Answer 1

The circle equation that has center , (1,-3) and passes through , (-6,-2) is given as
`(x-1)^2 + (y+3)^2  = 50`

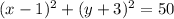
Explanation:

Here, the coordinate (h,k) of the center of circle = (1,-3)

Also, the point (x,y) on the circle = (-6,-2)

Let us assume the radius of the circle = r

The General equation of Circle is :
`(x-h)^2  + (y-k)^2  = (r)^2`

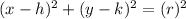
Substituting the value of (h,k) and (x,y) , we get:

`(-6-1)^2 + (-2-(-3))^2 = r^2\\\implies (-7)^2 + (-1)^2  = r^2\\\implies 49 + 1 = r^2\\\implies r= √(50)   = 7.07`

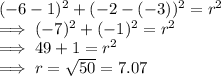
So, the radius of the circle = 7.07 units

Now, substitute the value of (h,k) = (1,-3) and r = 7.07 back in to the general circle equation, we get:

`(x-1)^2  + (y-(-3))^2  = (7.07)^2`

`\implies (x-1)^2 + (y+3)^2  = 50`

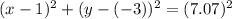
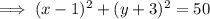
Hence, the circle equation that has center , (1,-3) and passes through , (-6,-2) is given as
`(x-1)^2 + (y+3)^2  = 50`