Question

A private and a public university are located in the same city. For the private university, 1038 alumni were surveyed and 647 said that they attended at least one class reunion. For the public university, 808 out of 1311 sampled alumni claimed they have attended at least one class reunion. Is the difference in the sample proportions statistically significant? (Use α=0.0

Answer 1

The problem asks to determine statistical significance between the proportions of alumni attending class reunions at a private vs public university using appropriate hypothesis testing.

Step-by-step explanation:

The question involves determining if there is a statistically significant difference in the sample proportions of alumni who have attended at least one class reunion at a private and a public university. To test for statistical significance, we calculate the difference between the two sample proportions and use a hypothesis test to compare this difference against the null hypothesis, which would suggest that there is no difference between the university proportions. Since a specific alpha level (significance level) is mentioned as α=0.05, we must check the calculated test statistic against the critical value for that alpha level to conclude whether the difference is significant or not.

Answer 2

The difference in the sample proportions is not statistically significant at 0.05 significance level.

Step-by-step explanation:

Significance level is missing, it is α=0.05

Let p(public) be the proportion of alumni of the public university who attended at least one class reunion

p(private) be the proportion of alumni of the private university who attended at least one class reunion

Hypotheses are:

`H_(0)`: p(public) = p(private)

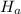`H_(a)`: p(public) ≠ p(private)

The formula for the test statistic is given as:

z=
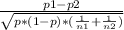`\frac{p1-p2}{\sqrt{{p*(1-p)*((1)/(n1) +(1)/(n2)) }}}` where

• p1 is the sample proportion of public university students who attended at least one class reunion (
  `(808)/(1311)=0.616`)

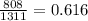• p2 is the sample proportion of private university students who attended at least one class reunion (
  `(647)/(1038)=0.623`)

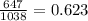• p is the pool proportion of p1 and p2 (
  `(808+647)/(1311+1038)=0.619`)

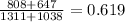• n1 is the sample size of the alumni from public university (1311)

• n2 is the sample size of the students from private university (1038)

Then z=
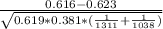`\frac{0.616-0.623}{\sqrt{{0.619*0.381*((1)/(1311) +(1)/(1038)) }}}` =-0.207

Since p-value of the test statistic is 0.836>0.05 we fail to reject the null hypothesis.