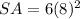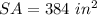1 Answer

Radek Anuszewski · Answer 1 · 2020-05-14T09:46:37+0000

Answer:

$SA=384\ in^2$

Explanation:

we know that

The smallest cube that could circumscribe the sphere has a length side equal to the diameter of the sphere

In this problem

The radius of the sphere is
$r=4\ in$

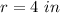
The diameter of the sphere is two times the radius

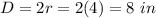
$D=2r=2(4)=8\ in$

so

The length side of the cube is

$b=8\ in$

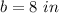
Remember that

The surface area of a cube is equal to the area of its six faces

so

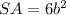
SA=6b^2

substitute the value of b

SA=6(8)^2

$SA=384\ in^2$

Please log in or register to add a comment.