Question

What this simplified

Answer 1

`\frac{3b\sqrt[3]{c^(2)} }{a^(2) }`

Explanation:

∛(27a⁻⁶b³c²)

To simplify, first apply the cube root the each of the terms. Keep in mind this rule:
`\sqrt[n]{a^(m)}  = (\sqrt[n]{a})^(m) = a^(m/n)`

∛27 = 3 (because 3*3*3 = 27)

∛a⁻⁶ =
`a^(-6/3)` =
`a^(-2)` =
`(1)/(a^(2))`

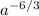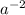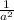
∛b³ =
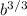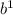`b^(3/3)` =
`b^(1)` = b

∛c² =
`c^(2/3)`

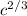
∛(27a⁻⁶b³c²)

=
`\frac{3b\sqrt[3]{c^(2)} }{a^(2) }`

Simplified form generally follows these rules:

No negative exponents

No fraction exponents

Keep in fractional form

Reduce numerical values