Question

A sample of impure tin of mass 0.538 g is dissolved in strong acid to give a solution of Sn2+. The solution is then titrated with a 0.0448 M solution of NO3−, which is reduced to NO(g). The equivalence point is reached upon the addition of 4.13×10−2 L of the NO3− solution.

Answer 1

The question is incomplete, here is a complete question.

A sample of impure tin of mass 0.538 g is dissolved in strong acid to give a solution of
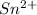`Sn^(2+)`. The solution is then titrated with a 0.0448 M solution of
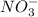`NO_3^-`, which is reduced to NO(g). The equivalence point is reached upon the addition of
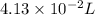`4.13* 10^(-2 )L` of the
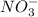`NO_3^-` solution.

Find the percent by mass of tin in the original sample, assuming that it contains no other reducing agents.

Answer : The percent mass of tin in the original sample is 61.3 %

Solution :

First we have to calculate the moles of
`NO_3^-`.

`\text{Moles of }NO_3^-=\text{Concentration of }NO_3^-* \text{Volume of solution}`

`\text{Moles of }NO_3^-=0.0448M* 4.13* 10^(-2)L=1.85* 10^(-3)mol`

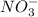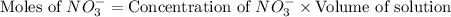
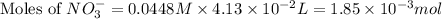
Now we have to calculate the moles of
`Sn^(4+)`

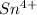
The balanced chemical reaction is,

`2NO_3^-(aq)+3Sn^(2+)(aq)+8H^+(aq)\rightarrow 2NO(g)+3Sn^(4+)(aq)+4H_2O(l)`

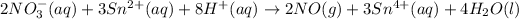
From the reaction, we conclude that

As, 2 mole of
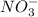`NO_3^-` react with 3 mole of
`Sn^(2+)`

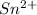
So,
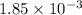`1.85* 10^(-3)` moles of
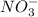`NO_3^-` react with
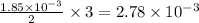`(1.85* 10^(-3))/(2)* 3=2.78* 10^(-3)` moles of
`Sn^(2+)`

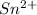
Now we have to calculate the mass of
`Sn^(2+)`

`\text{ Mass of }Sn^(2+)=\text{ Moles of }Sn^(2+)* \text{ Molar mass of }Sn^(2+)`

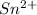
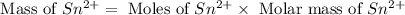
Molar mass of tin = 118.71 g/mol

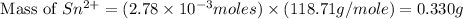
`\text{ Mass of }Sn^(2+)=(2.78* 10^(-3)moles)* (118.71g/mole)=0.330g`

Mass of
`Sn^(2+)` reacted = 0.330 g

Original mass of
`Sn^(2+)` = 0.538 g

Now we have to calculate the percent mass of tin in the original sample.

`\% \text{ mass of tin in the original sample}=\frac{\text{ Reacted mass of }Sn^(2+)}{\text{ Original mass of }Sn^(2+)}* 100`

`\% \text{ mass of tin in the original sample}=(0.330g)/(0.538g)* 100=61.3\%`

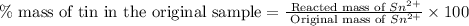
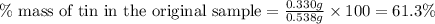
Therefore, the percent mass of tin in the original sample is 61.3 %