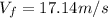Answer: 17.14 m/s
Step-by-step explanation:
We can solve this problem applying the Conservation of Mechanical energy (which is the sum of the kinetic energy
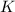 and potential energy
and potential energy
 ), where the total initial mechanical energy
), where the total initial mechanical energy
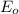 must be equal to the total final mechanical energy
must be equal to the total final mechanical energy
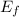 :
:
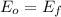 (1)
(1)
Being:
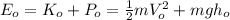 (2)
(2)
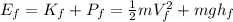 (3)
(3)
Where:
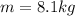 is the mass of the object
is the mass of the object
 is the initial velocity (the object was at rest)
is the initial velocity (the object was at rest)
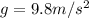 is the acceleration due gravity
is the acceleration due gravity
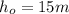 is the object's initial height or position
is the object's initial height or position
 is the final velocity
is the final velocity
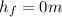 is the object's final height or position
is the object's final height or position
Solving and applying the given conditions:
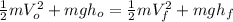 (4)
(4)
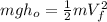 (5)
(5)
Finding
 :
:
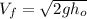 (6)
(6)
 (7)
(7)
Finally: