Question

A horizontal pipe 18.0 cm in diameter has a smooth reduction to a pipe 9.00 cm in diameter. If the pressure of the water in the larger pipe is 9.40 104 Pa and the pressure in the smaller pipe is 2.80 104 Pa, at what rate does water flow through the pipes?

Answer 1

The rate of flow of water is 71.28 kg/s

Solution:

As per the question:

Diameter, d = 18.0 cm

Diameter, d' = 9.0 cm

Pressure in larger pipe, P =
`9.40* 10^(4)\ Pa`

Pressure in the smaller pipe, P' =
`2.80* 10^(4)\ Pa`

Now,

To calculate the rate of flow of water:

We know that:

Av = A'v'

where

A = Cross sectional area of larger pipe

A' = Cross sectional area of larger pipe

v = velocity of water in larger pipe

v' = velocity of water in larger pipe

Thus

`\pi (d^(2))/(4)v = \pi (d'^(2))/(4)v'`

`18^(2)v = 9^v'`

v' = 4v

Now,

By using Bernoulli's eqn:

`P + (1)/(2)\rho v^(2) + \rho gh = P' + (1)/(2)\rho v'^(2) + \rho gh'`

where

h = h'

`\rho = 10^(3)\ kg/m^(3)`

`9.40* 10^(4) + (1)/(2)\rho v^(2) = 2.80* 10^(4) + (1)/(2)\rho (4v)^(2)`

`6.6* 10^(4)  = (1)/(2)\rho 15v^(2)`

`v = \sqrt{(2* 6.6* 10^(4))/(15* 10^(3))} = 8.8\ m/s`

Now, the rate of flow is given by:

`(dm)/(dt) = (d)/(dt)\rho Al = \rho Av`

`(dm)/(dt) = 10^(3)* \pi ((18)/(2)* 10^(- 2))^(2)* 8.8 = 71.28\ kg/s`

Answer 2

The rate of flow is 75.4 kg/s.

Step-by-step explanation:

Given that,

Diameter of pipe = 18.0 cm

Diameter = 9.00 cm

Pressure
`P= 9.40 *10^(4)\ Pa`

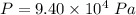
Pressure in the smaller pipe
`P'=2.80*10^(4)\ Pa`

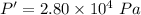
We need to calculate the velocity of longer pipe

Using formula of velocity

`A_(1)v_(1)=A_(2)v_(2)`

`\pi* r_(1)^2* v_(1)=\pi* r_(2)^2* v_(2)`

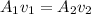
Put the value into the formula

`(9.00)^2* v_(1)=(4.5)^2* v_(2)^2`

`v_(1)=(20.25)/(81)* v_(2)`

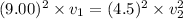
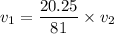
`v_(1)=0.25 v_(2)`....(I)

We need to calculate the velocity of smaller pipe

Using Bernoulli's equation

`P_(1)+(1)/(2)\rho* v^2+\rho g h=P_(2)+(1)/(2)\rho* v^2+\rho g h`

`P_(1)-P_(2)=(1)/(2)\rho(v_(2)^2-v_(1)^2)`

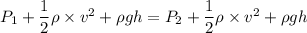
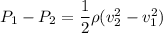
Put the value into the formula

`9.40 *10^(4)-2.80*10^(4)=(1)/(2)*1000(v_(2)^2-(0.25v_(2))^2)`

`6.6*10^(4)=(1)/(2)*1000*(0.9375)v_(2)^2`

`v_(2)^2=(2*6.6*10^(4))/(0.9375*1000)`

`v_(2)=\sqrt{(2*6.6*10^(4))/(0.9375*1000)}`

`v_(2)=11.86\ m/s`

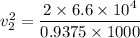
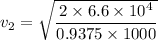
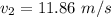
Put the value of v₂ in the equation (I)

`v_(1)=0.25*11.86`

`v_(1)=2.965\ m/s`

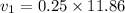
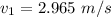
We need to calculate the flow

Using formula of flow rate

`Q=A_(2)* v_(2)`

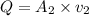
Where, Q = flow rate

A = area

v = velocity

Put the value into the formula

`Q=\pi*(4.5*10^(-2))^2*11.86`

`Q=0.0754\ m^3/s`

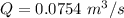
We need to calculate the rate of flow

Using formula of rate

`m=Q*\rho`

Put the value into the formula

`m=0.0754*1000`

`m=75.4\ kg/s`

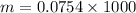
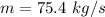
Hence, The rate of flow is 75.4 kg/s.