Question

The population of a colony of mosquitoes obeys the law of uninhibited growth. If there are 1000 mosquitoes initially and there are 1900 after 1​ day, what is the size of the colony after 4 ​days? How long is it until there are 60 comma 000 ​mosquitoes?

Answer 1

a) 13032

b)6.4 days

Explanation:

The formula for the population growth is given by

`A=Pe^(rt)`

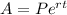
Here, A = final population, P = initial population, r = growth rate and t = time

From the given directions, we have

A = 1900, P = 1000, t = 1, r = ?

Substituting these values in the above formula to find r

`1900=1000e^(r\cdot1)\\\\1900=1000e^r`

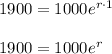
Divide both sides by 1000

`(1900)/(1000)=e^r\\\\e^r=(19)/(10)`

Take natural log both sides

`\ln(e^r)=\ln((19)/(10))\\\\r=0.64185`

Therefore, the population model is given by

`A=1000e^(0.64185t)`

(a) The size of the colony after 4 ​days is given by

`A=1000e^(0.64185\cdot4)\\\\A=13032`

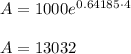
(B) The time for the number of mosquitoes to be 60,000 is

`60000=1000e^(0.64185t)`

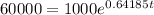
Divide both sides by 1000

`(60000)/(1000)=e^(0.64185t)\\\\e^(0.64185t)=60`

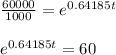
Take natural log both sides

`\ln(e^(0.64185t))=\ln60\\\\0.64185t=\ln60\\\\t=(\ln60)/(0.64185)\\\\t=6.4`

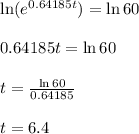
Hence, it will take 6.4 days to the population of mosquitoes to be 60000.