Answer:
(a) P(x>125)=0.0478
(b) p(90<x<110)=0.4950
Explanation:
Normal Distribution
It's a probability distribution used to model the behavior of random events where most of the observations lie close to the central peak (or top of the bell curve).
The normal distribution uses two parameters: the standard deviation
 and the mean
and the mean
 . The cumulative probabilities are usually given in pre-computed tables, graphs or provided by digital means, like Excel. The procedure to find probabilities of intervals of random values of X is to use the normalized curve which entry is a parameter called the z-score or standard normal deviate
. The cumulative probabilities are usually given in pre-computed tables, graphs or provided by digital means, like Excel. The procedure to find probabilities of intervals of random values of X is to use the normalized curve which entry is a parameter called the z-score or standard normal deviate
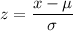
The parameters needed to find the required probabilities are
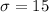 and
and

a) To know the probability that the score of a person is more than 125, we enter in the Excel function NORMDIST(125,100,15, TRUE). The first 3 parameters are obvious, the last one is to indicate if Excel should return the cumulative probability.
The value returned by this function is
P(x<125)=0.9522
Note this function returns the left-tail cummulative probability. To know the values greater than x=125, we just subtract from 1
P(x>125)=1-0.9522=0.0478
b) The probability that the score is between 90 and 110 will be computed in three parts. First we calculate p(x<90), then p(x<110) and finally we subtract those values
p(x<90)=NORMDIST(90,100,15,TRUE)=0.2525
p(x<110)=NORMDIST(110,100,15,TRUE)=0.7475
p(90<x<110)=0.7475-0.2525=0.4950