Question

A recent report claimed that Americans are retiring later in life ( U.S. News & World Report, August 17). An economist wishes to determine if the mean retirement age has increased from 62. To conduct the relevant test, she takes a random sample of 38 Americans who have recently retired and computes the value of the test statistic as t 37 = 1.92. With α = 0.05, she ________.

Answer 1

If we compare the p value and a significance level given
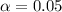`\alpha=0.05` we see that
`p_v<\alpha` so we can conclude that we can reject the null hypothesis, and the actual true mean is significanlty higher than 62 at 5% of significance.

Explanation:

Data given and notation

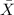`\bar X` represent the sample mean

`s` represent the standard deviation for the sample

`n=38` sample size

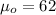`\mu_o =62` represent the value that we want to test

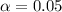`\alpha=0.05` represent the significance level for the hypothesis test.

t would represent the statistic (variable of interest)

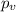`p_v` represent the p value for the test (variable of interest)

State the null and alternative hypotheses to be tested

We need to conduct a hypothesis in order to determine if the mean is higher than 62, the system of hypothesis would be:

Null hypothesis:
`\mu \leq 62`

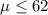
Alternative hypothesis:
`\mu > 62`

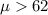
Compute the test statistic

We don't know the population deviation, so for this case is better apply a t test to compare the actual mean to the reference value, and the statistic is given by:

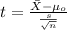`t=(\bar X-\mu_o)/((s)/(√(n)))` (1)

t-test: "Is used to compare group means. Is one of the most common tests and is used to determine if the mean is (higher, less or not equal) to an specified value".

The t statisitc for this case we got t=1.92

Now we need to find the degrees of freedom for the t distirbution given by:

`df=n-1=38-1=37`

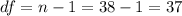
Compute the p-value

Since is a one right tailed test the p value would be:

`p_v =P(t_(37)>1.92)=0.0313`

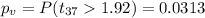
If we compare the p value and a significance level given
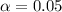`\alpha=0.05` we see that
`p_v<\alpha` so we can conclude that we can reject the null hypothesis, and the actual true mean is significanlty higher than 62 at 5% of significance.