Question

You are spinning a spinner labeled 1-5 and you choose a marble out of the bag of 7 marbles, 2 are blue, 3 are red, 1 is green and 1 is black. What is the probability of the following: P(spinning a 3 and choosing a red) Leave your answer as a UNREDUCED fraction

Answer 1

`\text{P(spinning a 3 and choosing a red)}=(3)/(70)`

Explanation:

It has been given that you are spinning a spinner labeled 1-5 and you choose a marble out of the bag of 7 marbles, 2 are blue, 3 are red, 1 is green and 1 is black.

`\text{Probability}=\frac{\text{Number of favorable outcomes}}{\text{Total number of possible outcomes}}`

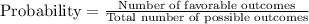
The probability of spinning a 3 would be:
`(1)/(5)`.

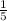The probability of choosing a red would be:

`\text{P(Red)}=\frac{\text{Number of red marbles}}{\text{Total number of marbles}}`

`\text{P(Red)}=(3)/(7+2+3+1+1)`

`\text{P(Red)}=(3)/(14)`

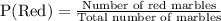
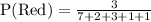
Since both events are independent, so probability of spinning a 3 and choosing a red marble would be probability of spinning a 3 times probability of choosing a red marble.

`\text{P(spinning a 3 and choosing a red)}=\text{P(spinning a 3)}* \text{P(Choosing a red)}`

`\text{P(spinning a 3 and choosing a red)}=(1)/(5)* (3)/(14)`

`\text{P(spinning a 3 and choosing a red)}=(1* 3)/(5* 14)`

`\text{P(spinning a 3 and choosing a red)}=(3)/(70)`

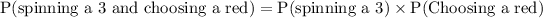
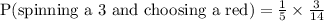
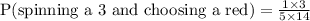
Therefore, the probability of spinning a 3 and choosing a red marble would be
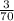`(3)/(70)`.