Question

A diver named Jacques observes a bubble of air rising from the bottom of a lake (where the absolute pressure is 3.50 atm) to the surface (where the pressure is 1.00 atm). The temperature at the bottom is 4.0 ∘C, and the temperature at the surface is 23.0 ∘C.

a. What is the ratio of the volume of the bubble as it reaches the surface (Vs) to its volume at the bottom (Vb)?
b. Would it be safe for Jacques to hold his breath while ascending from the bottom of the lake to the surface?

Answer 1

3.73994

No,

Step-by-step explanation:

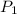`P_1` = Pressure at the bottom of the lake = 3.5 atm

`P_2` = Pressure at the top of the lake = 1 atm

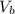`V_b` = Volume at the bottom of the lake

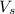`V_s` = Volume at the top of the lake

`T_1` = Temperature at the bottom of the lake = 4 °C

`T_2` = Temperature at the top of the lake = 23 °C

From ideal gas law we have the relation

`(P_1V_b)/(T_1)=(P_2V_s)/(T_2)\\\Rightarrow (V_b)/(V_s)=(P_2T_1)/(P_1T_2)\\\Rightarrow (V_b)/(V_s)=(1* 277.15)/(3.5* 296.15)\\\Rightarrow (V_s)/(V_b)=0.26738^(-1)\\\Rightarrow (V_s)/(V_b)=3.73994`

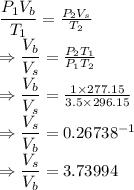
The ratio is 3.73994

As Jacques is ascending if he holds his breath his lungs acting like a bubble would expand. Hence, it is not safe to hold his breath while ascending,