Question

Evaluate cube root of 5 multiplied by square root of 5 over cube root of 5 to the power of 5.

a
5 to the power of negative 1 over 6

b
5 to the power of 3 over 2

c
5 to the power of 5 over 2

d
5 to the power of negative 5 over 6

Answer 1

Option d) 5 to the power of negative 5 over 6 is correct.

`\frac{\sqrt[3]{\bf 5} * √(\bf 5)}{\sqrt[3]{\bf 5^(\bf 5)}}= 5^{(\bf -5)/(\bf 6)}`

Above equation can be written as 5 to the power of negative 5 over 6.

ie,
`5^(\bf -5)/(\bf 6)`

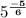
Explanation:

Given that cube root of 5 multiplied by square root of 5 over cube root of 5 to the power of 5.

It can be written as below

`\frac{\sqrt[3]{5} * √(5)}{\sqrt[3]{5^5}}`

`\frac{\sqrt[3]{5} * √(5)}{\sqrt[3]{5^5}}= \frac{5^{(1)/(3)} * 5^{(1)/(2)}}{5^{(5)/(3)}}`

`\frac{\sqrt[3]{5} * √(5)}{\sqrt[3]{5^5}}= \frac{5^{(1)/(3)+(1)/(2)}}{5^{(5)/(3)}}`

`\frac{\sqrt[3]{5} * √(5)}{\sqrt[3]{5^5}}= \frac{5^{(2+3)/(6)}}{5^{(5)/(3)}}`

`\frac{\sqrt[3]{5} * √(5)}{\sqrt[3]{5^5}}= 5^{(5)/(6)} * 5^{(-5)/(3)}`

`\frac{\sqrt[3]{5} * √(5)}{\sqrt[3]{5^5}}= 5^{(5-10)/(6)}`

`\frac{\sqrt[3]{5} * √(5)}{5^5}= 5^{(-5)/(6)}`

Above equation can be written as 5 to the power of negative 5 over 6.