Question

A boat traveled 147 miles downstream and back. The trip downstream took 7 hours. The trip back took 147 hours. Find the speed of the boat in still water and the speed of the current.

Answer 1

The speed of boat in still water is 11 miles per hour

The speed of current is 10 miles per hour .

Explanation:

Given as :

The distance cover by boat in downstream =
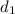`d_1` = 147 miles

The time taken by boat in downstream trip =
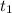`t_1` = 7 hours

The distance cover by boat in upstream =
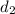`d_2` = 147 miles

The time taken by boat in upstream trip =
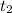`t_2` = 147 hours

Let The speed of boat in still water =
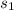`s_1` = x mph

And The speed of the current =
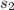`s_2` = y mph

Now, According to question

Speed =
`(\textrm Distance)/(\textrm Time)`

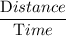
For downstream

`s_1` +
`s_2` =
`(d_1)/(t_1)`

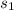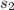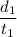
or, x + y =
`(147)/(7)`

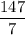
I.e x + y = 21 mph ..........1

For upstream

`s_1` +
`s_2` =
`(d_2)/(t_2)`

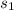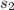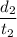
or, x - y =
`(147)/(147)`

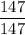
I.e x - y = 1 mph ..........2

Now, Solving Eq 1 and 2

I.e (x + y) + (x - y) = 21 + 1

Or, (x + x) + (y - y) = 22

Or, 2 x = 22

∴ x =
`(22)/(2)`

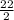
I.e x = 11 mph

So, speed of boat = x = 11 miles per hour

Again, put The value of x in Eq 2

So, x - y = 1 mph

I.e 11 - y = 1

∴, y = 11 - 1

I.e y = 10 mph

So, speed of current = y = 10 miles per hour

Hence The speed of boat in still water is 11 miles per hour , and The speed of current is 10 miles per hour . Answer