Question

The ceiling of your lecture hall is probably covered with acoustic tile, which has small holes separated by about 5.9 mm. Using light with a wavelength of 527 nm, how far could you be from this tile and still resolve these holes? The diameter of your eye is about 5 mm.( )mCould you resolve these holes better with red light or with violet light? (You have only 1 try.)1. violet.2. red

Answer 1

45.88297 m

Violet

Step-by-step explanation:

x = Gap between holes = 5.9 mm

`\lambda` = Wavelength = 527 nm

D = Diameter of eye = 5 mm

L= Distance of observer from holes

From Rayleigh criteria we have the relation

`(x)/(L)=1.22(\lambda)/(D)\\\Rightarrow L=(xD)/(1.22\lambda)\\\Rightarrow L=(5.9* 10^(-3)* 5* 10^(-3))/(1.22* 527* 10^(-9))\\\Rightarrow L=45.88297\ m`

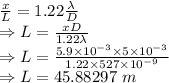
A person could be 45.88297 m from the tile and still resolve the holes

Resolving them better means increasing the distance between the observer and the holes. It can be seen here that the distance is inversely proportional to the wavelength. Violet has a lower wavelength than red so, violet light would resolve the holes better.