Question

A stockroom worker pushes a box with mass 11.4 kg on a horizontal surface with a constant speed of 2.90 m/s . The coef­ficients of kinetic and static friction between the box and the surface are 0.260 and 0.550, respectively. a. What horizontal force must the worker apply to maintain the motion of the box?b. If the worker stops pushing, what will be the acceleration of the box?

Answer 1

29.07684 N

-2.5506 m/s²

Step-by-step explanation:

m = Mass of box = 11.4 kg

g = Acceleration due to gravity = 9.81 m/s²

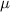`\mu` = Coef­ficient of kinetic friction = 0.26

N = Normal force =
`mg`

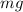
Frictional force is given by

`f=\mu N\\\Rightarrow f=0.26* 11.4* 9.81\\\Rightarrow f=29.07684\ N`

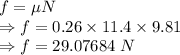
The horizontal force required to push the box is 29.07684 N

Acceleration is given by

`a=-(f)/(m)\\\Rightarrow a=-(\mu mg)/(m)\\\Rightarrow a=-\mu g\\\Rightarrow a=-0.26* 9.81\\\Rightarrow a=-2.5506\ m/s^2`

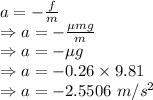
The acceleration of the box is -2.5506 m/s²