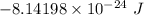Answer:
1836214271.77724 kg/m³
3268476.80175 m/s²
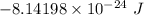
Step-by-step explanation:
m = Mass of Sun =
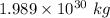
r = Radius of Earth = 6371000 m
Volume of Earth
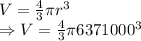
Density is given by
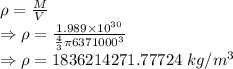
Density of the Sun would be 1836214271.77724 kg/m³
Acceleration due to gravity is given by
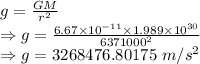
Acceleration due to gravity on the Sun would be 3268476.80175 m/s²
Potential energy is given by

The gravitational potential energy associated with the object is