Question

10.106 Public Health and Nutrition Over the last decade, many Americans have been able to stop smoking. However, a recent survey suggests that asthmatic children are more likely to be exposed to second-hand smoke than children without asthma.19 In a random sample of 300 children without asthma, 132 were regularly exposed to second-hand smoke, and in a random sample of 325 children with asthma, 177 were regularly exposed to second-hand smoke. Is there any evidence to suggest that the proportion of children with asthma who are exposed to second-hand smoke is greater than the proportion for children without asthma? Use a 5 0.01.

Answer 1

There is no significant evidence at 0.01 significance level, to suggest that the proportion of children with asthma who are exposed to second-hand smoke is greater than the proportion for children without asthma

Explanation:

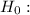`H_(0):` the proportion of children with asthma who are exposed to second-hand smoke is equal the proportion for children without asthma

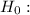`H_(0):` the proportion of children with asthma who are exposed to second-hand smoke is greater than the proportion for children without asthma

Test statistic can be calculated using the formula

z=
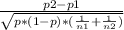`\frac{p2-p1}{\sqrt{{p*(1-p)*((1)/(n1) +(1)/(n2)) }}}` where

• p1 is the proportion of children without asthma who are exposed to second-hand smoke (
  `(132)/(300)=0.440` )

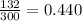• p2 is the proportion of children with asthma who are exposed to second-hand smoke (
  `(177)/(325)=0.545` )

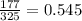• p is the pool proportion of p1 and p2 (
  `(132+177)/(300+325)=0.494`)

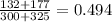• n1 is the sample size of children without asthma (300)

• n2 is the sample size of children with asthma (325)

Then z=
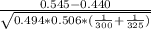`\frac{0.545-0.440}{\sqrt{{0.494*0.506*((1)/(300) +(1)/(325)) }}}` ≈1.679

P-value of test statistic is ≈0.047. Since 0.047>0.01 (significance level) we fail to reject the null hypothesis.