Question

What is tan 3pi/4?

A. -1
B. |2|/2
C. -|2|/2
D. |3|/2

Answer 1

tan 3pi/4 is equal to -1

Solution:

Given that we have to find value of
`\tan (3 \pi)/(4)`

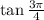
Let us evaluate the given expression

`\tan (3 \pi)/(4)=\tan \left(\pi-(\pi)/(4)\right)`

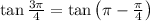
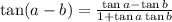`\tan (a-b)=(\tan a-\tan b)/(1+\tan a \tan b)` ---- eqn 1

`\text{In} \tan \left(\pi-(\pi)/(4)\right), a=\pi \text { and } b=(\pi)/(4)`

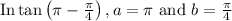
Substituting the values in eqn 1,

`\tan \left(\pi-(\pi)/(4)\right)=(\tan \pi-\tan (\pi)/(4))/(1+\tan \pi \tan (\pi)/(4))`

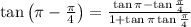
we know that by trignometric values,

`\tan \pi=0 \text { and } \tan (\pi)/(4)=1`

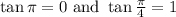
Substituting these values we get,

`\tan \left(\pi-(\pi)/(4)\right)=(0-1)/(1+0(1))=(-1)/(1)=-1`

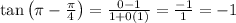
Therefore,

`\tan \left(\pi-(\pi)/(4)\right)=\tan (3 \pi)/(4)=-1`

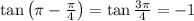
Thus the value of tan 3pi/4 is -1