Question

A person on a rocket traveling at 0.47 c (with respect to the Earth) observes a meteor come from behind and pass her at a speed she measures as0.47 c.

How fast is the meteor moving with respect to the Earth?

Answer 1

The concept to solve this problem is related to the relativistic physics for which the speed of the object in different frames of reference is related. This concept is called Velocity-addition formula

and can be written as,

`u = (v+u')/(1+(vu')/(c^2))`

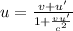
Where,

u = Velocity of a body within a Lorentz Frame

v = Velocity of a second frame

u'= The transformed velocity of the body within the second frame

c = speed of light

Replacing we have to

`u = (v+u')/(1+(vu')/(c^2))`

`u = (0.47c+0.47c)/(1+(0.47c*0.47c)/(c^2))`

`u = 0.769c`

`u \approx 230'700.000m/s`

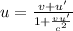
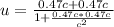
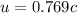
Therefore the meteor moving with respect to the Earth to 230'700.000m/s