Question

Cesium-137 undergoes beta decay and has a half-life of 30.0 years. How many beta particles are emitted by a 14.0-g sample of cesium-137 in three minutes?

Answer 1

Answer:
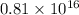`0.81* 10^(16)` beta particles

Step-by-step explanation:

`\text{Number of moles}=\frac{\text{Given mass}}{\text{Molar mass}}`

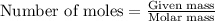
Given mass = 14.0 g

Molar mass = 137 g/mol

`\text{Number of moles of cesium}=(14.0g)/(137g/mol)=0.102moles`

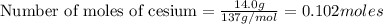
According to avogadro's law, 1 mole of every substance weighs equal to its molecular mass and contains avogadro's number
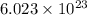`6.023* 10^(23)` of particles.

1 mole of cesium contains atoms =
`6.023* 10^(23)`

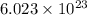
0.102 moles of cesium contains atoms =
`(6.023* 10^(23))/(1)* 0.102=0.614* 10^(23)`

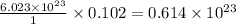
The relation of atoms with time for radioactivbe decay is:

`N_t=N_0* (1)/(2)^{\frac{t}{t_{(1)/(2)}}}`

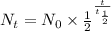
Where
`N_t` =atoms left undecayed

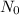`N_0` = initial atoms

t = time taken for decay = 3 minutes

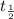`{t_{(1)/(2)}}` = half life = 30.0 years =
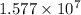`1.577* 10^7` minutes

The fraction that decays :
`1-((1)/(2))^{(3)/(1.577* 10^7)}=1.32* 10^(-7)`

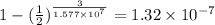
Amount of particles that decay is =
`0.614* 10^(23)* 1.32* 10^(-7)=0.81* 10^(16)`

Thus
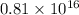`0.81* 10^(16)` beta particles are emitted by a 14.0-g sample of cesium-137 in three minutes.