Question

Which of these points lies on the line described by the equation below?

y- 4 = -2(x-6)
O A. (-6,-4)
O B. (6,4)
O c. (-4,-6)
O D. (4, 6)
Help plzzz?

Answer 1

B. (6, 4)

Explanation:

The slope-point form of an equation of a line:

`y-y_1=m(x-x_1)`

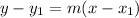
m - slope

(x₁, y₁) - point on a line

We have the equation:

`y-4=-2(x-6)`

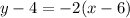
hence

`m=-2,\ x_1=6,\ y_1=4\to(6,\ 4)`

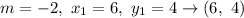
Check other points:

Substitute the coordinates of the points into the equation and check the equality:

A. (-6, -4)

-4 - 4 = -2(-6 - 6)

-8 = 24 FALSE

C. (-4, -6)

-6 - 4 = -2(-4 - 6)

-10 = 20 FALSE

D. (4, 6)

6 - 4 = -2(4 - 6)

2 = 4 FALSE