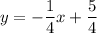Answer:
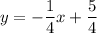
Explanation:
You solve a question like this by finding the slope and intercept of the desired line and putting those values into the answer form.
__
The relationship between slopes of perpendicular lines is that one is the negative reciprocal of the other.
The slope-intercept form of the equation for a line is ...
y = mx + b . . . . . . where m is the slope and b is the y-intercept
The given line is in "slope-intercept form," so you can identify the slope as 4 and the y-intercept as 6. (For this question, the y-intercept of the given line is irrelevant.)
Using the relationship between slopes of perpendicular lines, you now know the slope of the line you want is m = -1/(slope of given line) = -1/4. This is the coefficient of x in the slope-intercept form, so fills the blanks on the left.
To make the line go through the point (1, 1), you need to choose a y-intercept that makes (x, y) = (1, 1) a solution to the equation. For a y-intercept of "b", that means ...
y = -1/4x + b
1 = -1/4·1 + b . . . . . . . . fill in the values of x and y at the given point
1 + 1/4 = b = 5/4 . . . . . add 1/4 to both sides of the equation
Now you know the equation you want is ...