Question

An airplane has an effective wing surface area of 17.0 m2 that is generating the lift force. In level flight the air speed over the top of the wings is 55.0 m/s, while the air speed beneath the wings is 40.0 m/s. What is the weight of the plane?

Answer 1

To solve this problem it is necessary to apply the equations given from Bernoulli's principle, which describes the behavior of a liquid moving along a streamline. Mathematically this expression can be given as,

`P_1 + (1)/(2)\rho*v_1^2 + P_2 + (1)/(2)*\rho*v_2^2=0`

Where,

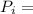`P_i =` Pressure at each state

`\rho`= Density

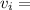`v_i =` Velocity

Re-organizing the expression we can get that

`P_1 - P_2 = (1)/(2)\rho (v_2^2 - v_1^2)`

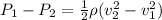
Our values are given as

`v_1 = 40m/s`

`v_2 = 55m/s`

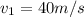
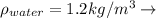`\rho_(water) = 1.2kg/m^3 \rightarrow` Normal Conditions

Replacing we have,

`P_1 -P_2 = (1)/(2)*1.2*(55^2-40^2)`

`P_1 - P_2 = 855Pa`

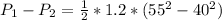
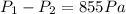
If we consider that there is a balance between the two states, the Force provided by gravity is equivalent to the Support Force, therefore

`F_l = F_g`

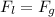
Here the lift force is the product between the pressure difference previously found by the effective area of the aircraft, while the Force of gravity represents the weight. There,

`F_g = W`

`F_l = (P_2-P_1)A`

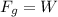
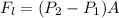
Equating,

`(P_1 - P_2)*A = W`

`W = 855*17`

`W = 14535 N`

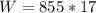
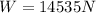
Therefore the weight of the plane is 14535N