1 Answer

Cristis · Answer 1 · 2020-10-18T06:51:24+0000

The equation for the linear function whose graph contains the points (-1, -2) and (3, 10) is y = 3x + 1

Given that linear function whose graph contains the points (-1, -2) and (3, 10)

We have to find the equation of line

Any function of the form f (x) = m x + b, where m is not equal to 0 is called a linear function

So let us use the slope intercept form

The slope intercept form is given as:

y = mx + c

Where "m" is the slope of line and "c" is the y - intercept

Let us first find slope of line containing points (-1, -2) and (3, 10)

The slope of line is given as:

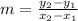
m=(y_(2)-y_(1))/(x_(2)-x_(1))

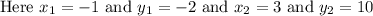
$\text {Here } x_(1)=-1 \text { and } y_(1)=-2 \text { and } x_(2)=3 \text { and } y_(2)=10$

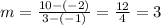
m=(10-(-2))/(3-(-1))=(12)/(4)=3

Thus the slope of line is "m" = 3

Substitute m = 3 and (x, y) = (-1, -2) in y = mx + c

-2 = 3(-1) + c

-2 = -3 + c

c = -2 + 3 = 1

Now substitute c = 1 and m = 3 in slope intercept form to get equation of line

y = 3x + 1

Thus the equation for the linear function is found out

Please log in or register to add a comment.