Question

A model rocket is launched at an angle of 70° above the x axis, with an initial velocity of 40 m/s. What is the maximum height the rocket will reach?

A. 34.7m
B. 72.1m
C. 81.6m
D. 95.4m​

Answer 1

maximum height is 72.09 m which can be rounded to 72.1 m (Answer B)

Step-by-step explanation:

In order to analyze the vertical motion and the maximum height the rocket reaches, we need to know the vertical component of the velocity at launch. That can be estimated knowing the launching angle of 70 degrees using right angle trigonometry:

`v_y=40\,*\,sin(70^o)\\v_y=37.59\,(m)/(s)`

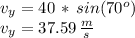
We recall that when the rocket reaches it maximum vertical height, its vertical component of the velocity is zero, and from then on, the trajectory of the rocket is going to go downwards accelerated by the action of gravity. We can use the following equation that relates initial and final velocities, acceleration (g), and distance traveled (final vertical position minus initial):

`v_f^2-v_i^2=2\,a\,(y_f-y_i)\\0-37.59^2=2\,(-9.8)\,(y_f-y_i)\\(-1413)/(-19.6) =(y_f-y_i)\\72.09\,m=(y_f-y_i)\\(y_f-0)=72.09\,m\\y_f=72.09\,m`

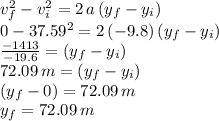
This is therefore the maximum height at the end of the upwards motion, when the vertical component of the velocity becomes zero.