Question

To the nearest tenth, find the perimeter of triangle ABC with vertices A(3, 2), B(-2, 3), and C(2, 6)

Answer 1

14.2 units

Explanation:

To find the distance between the points, you use the formula

`d = \sqrt {(x_1 - x_2)^(2) + (y_1 - y_2)^(2)}`

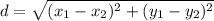
Therefore, we need to get the distances between points A and B, between points B and C and between points A and C.

Length
`AB=\sqrt {(3--2)^(2)+(2-3)^(2)}=\sqrt 26\\BC=\sqrt{(2--2)^(2)+(6-3)^(2)}=5\\AC=\sqrt {(2-3)^(2)+(6-2)^(2)}=\sqrt 17\\`

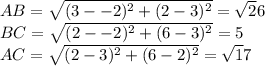
Perimeter=
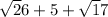`\sqrt 26+5+\sqrt 17`=14.2 units (to the nearest tenth)