Question

The production manager for the XYZ manufacturing company is concerned that the customer orders are being shipped late. He asked one of his planners to check the timeliness of shipments for 900 orders. The planner randomly selected 900 orders and found that 180 orders were shipped late. Construct the 95% confidence interval for the proportion of orders shipped late.

Answer 1

The 95% confidence interval would be given (0.174;0.226).

We are confident (95%) that true proportion of orders that were shipped late is between 0.174 and 0.226

Explanation:

Data given and notation

n=900 represent the random sample taken

X=180 represent the orders that were shipped late

`\hat p=(180)/(900)=0.2` estimated proportion of the orders that were shipped late

`\alpha=0.05` represent the significance level (no given, but is assumed)

p= population proportion of orders that were shipped late

The confidence interval would be given by this formula

`\hat p \pm z_(\alpha/2) \sqrt{(\hat p(1-\hat p))/(n)}`

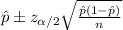
For the 95% confidence interval the value of
`\alpha=1-0.95=0.05` and
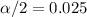`\alpha/2=0.025`, with that value we can find the quantile required for the interval in the normal standard distribution.

`z_(\alpha/2)=1.96`

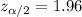
And replacing into the confidence interval formula we got:

`0.2 - 1.96 \sqrt{(0.2(1-0.2))/(900)}=0.174`

`0.2 + 1.96 \sqrt{(0.2(1-0.2))/(900)}=0.226`

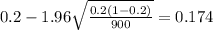
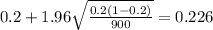
And the 95% confidence interval would be given (0.174;0.226).

We are confident (95%) that true proportion of orders that were shipped late is between 0.174 and 0.226