Question

In the winter activity of tubing, riders slide down snow covered slopes while sitting on large inflated rubber tubes. To get to the top of the slope, a rider and his tube, with a total mass of 84 kg , are pulled at a constant speed by a tow rope that maintains a constant tension of 350 N .

Answer 1

17304 J

Step-by-step explanation:

Since there are no springs or chemical reactions involved the work-energy equation is

W = ΔK + ΔUg + ΔEth

We are told the towing takes place at a constant speed so ΔK = 0. Solve for the change in thermal energy.

ΔEth = W - ΔUg = Fd -mgΔy

ΔEth = (350)(120) - (84)(9.8)(30)

ΔEth = 17304 J

Answer 2

17304 J

Step-by-step explanation:

Complete statement of the question is :

In the winter activity of tubing, riders slide down snow covered slopes while sitting on large inflated rubber tubes. To get to the top of the slope, a rider and his tube, with a total mass of 84 kg , are pulled at a constant speed by a tow rope that maintains a constant tension of 350 N .

Part A

How much thermal energy is created in the slope and the tube during the ascent of a 30-m-high, 120-m-long slope?

Solution :

`T` = tension force in the tow rope = 350 N

`L` = length of the incline surface = 120 m

`W_(t)` = work done by tension force = ?

The tension force acts parallel to incline surface, hence work done by tension force is given as

`W_(t) = T L\\W_(t) = (350) (120)\\W_(t) = 42000 J`

`h` = height gained by the rider = 30 m

`m` = total mass of rider and tube = 84 kg

Potential energy gained is given as

`U = mgh\\U = (84) (9.8) (30)\\U = 24696 J`

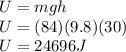
`Q` = Thermal energy created

Using conservation of energy

`Q = W_(t) - U\\Q = 42000 - 24696\\Q = 17304 J`