Question

A company’s total cost from manufacturing and selling x units of their product is given by: y = 2x2 – 600x + 49,000. How many units should be manufactured in order to minimize cost, and what is the minimum cost?a. (100, $9,000)b. (125, $3,250)c. (150, $4,000)d. (170, $4,800)e. (200, $9,000)

Answer 1

Answer: Option 'c' is correct.

Explanation:

Since we have given that

`y=2x^2-600x+49000`

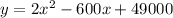
We need to find the number of units in order to minimize cost.

We first derivative w.r.t. x,

`y'=4x-600`

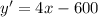
For critical points:

`y'=0\\\\4x-600=0\\\\4x=600\\\\x=(600)/(4)\\\\x=150`

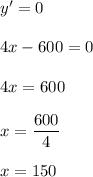
Now, we will check whether it is minimum or not.

We will find second derivative .

`y''=4>0`

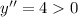
So, it will yield minimum cost.

Minimum cost would be

`y(150)=2(150)^2-600* 150+49000\\\\y(150)=\$4000`

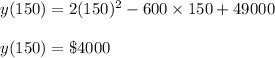
Hence, At 150 units, minimum cost = $4000

Therefore, Option 'c' is correct.