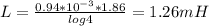Answer:
PartA) resistance R=1.86Ω
PartB) inductnce L=1.26mH
Step-by-step explanation:
In an RL circuit,
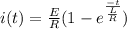
where E is the emf of battery
L is inductance of inductor
R is the internal resistance of inductor
given
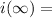
 max=
max=
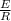
⇒
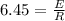
⇒
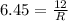
⇒
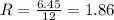 Ω
Ω
given

⇒

⇒
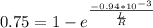
⇒
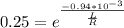
applying logarithm on both sides,
⇒
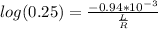
⇒
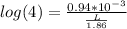
⇒