Answer:
x=199 and y=158
Step-by-step
Let x and y be two numbers
Given that the sum of the two numbers is 357, it may be written as

difference of the two numbers is 41, it may be written as

Now adding (1) and (2), we get
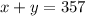
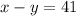
_______________________________________
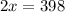
_______________________________________
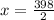 (Where y is in alternative signs so it may be cancelled)
(Where y is in alternative signs so it may be cancelled)
Therefore
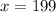
now substituting x=199 in (1) we get
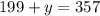
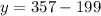
Therefore
