Question

Find the equation of the axis of symmetry of the following parabola algebraically.

y=-x^2+12x-38

Answer 1

the independent variable is the one that's squared, namely the "x", that means that the parabola is a vertically opening parabola, so its axis of symmetry will simply be the equation of the vertical line that passes through the vertex, hmmm what's its vertex anyway?

`\textit{vertex of a vertical parabola, using coefficients} \\\\ y=\stackrel{\stackrel{a}{\downarrow }}{-1}x^2\stackrel{\stackrel{b}{\downarrow }}{+12}x\stackrel{\stackrel{c}{\downarrow }}{-38} \qquad \qquad \left(-\cfrac{ b}{2 a}~~~~ ,~~~~ c-\cfrac{ b^2}{4 a}\right)`

`\left(-\cfrac{ 12}{2(-1)}~~~~ ,~~~~ -38-\cfrac{ (12)^2}{4(-1)}\right) \implies \left( - \cfrac{ 12 }{ -2 }~~,~~-38 - \cfrac{ 144 }{ -4 } \right) \\\\\\ (6~~,~~-38+36)\implies (\stackrel{x}{6}~~,~~-2)~\hfill \stackrel{\textit{axis of symmetry}}{x=6}`

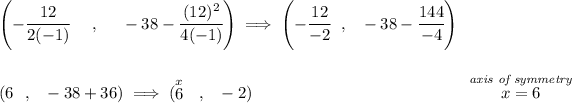
Check the picture below.