Question

I need the answer for this exact question

Answer 1

`y=(7)/(2)x-20`

Explanation:

Let the equation of the line be
`y-y_1=m(x-x_1)` where, 'm' is its slope and
`(x_1,y_1)` is a point on it.

Given:

The equation of a known line is:

`y=-(2)/(7)x+9`

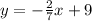
A point on the unknown line is:

`(x_1,y_1)=(4,-6)`

Both the lines are perpendicular to each other.

Now, the slope of the known line is given by the coefficient of 'x'. Therefore, the slope of the known line is
`m_1=-(2)/(7)`

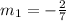
When two lines are perpendicular, the product of their slopes is equal to -1.

Therefore,

`m\cdot m_1=-1\\m=-(1)/(m_1)\\m=-(1)/((-2)/(7) )=(7)/(2)`

Therefore, the equation of the unknown line is determined by plugging in all the given values. This gives,

`y-(-6))=(7)/(2)(x-4)\\y+6=(7)/(2)x-14\\y=(7)/(2)x-14-6\\\\y=(7)/(2)x-20`

The equation of a line perpendicular to the given line and passing through (4, -6) is
`y=(7)/(2)x-20`.