Question

SOLVE USING LONG DIVISION:

(3x^2+7x-20) / (x+4)

please show work on paper , it'll be more helpful

Answer 1

`(3x^2+7x-20)/(x+4)=3x-5`

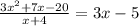
Explanation:

Long division:

Step 1:

We divide '3x²' by 'x' to get the first term of quotient.

⇒
`(3x^2)/(x)=3x`

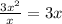
Now, we multiply '3x' to
`(x+4)`

⇒
`3x(x+4)=3x^2+12x`

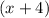
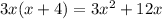
Now, we subtract
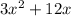`3x^2+12x` from the given numerator
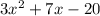`3x^2+7x-20`. This gives,

`=3x^2+7x-20-(3x^2+12x)\\=3x^2+7x-20-3x^2-12x\\=3x^2-3x^2+7x-12x-20\\=-5x-20`

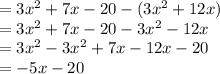
Step 2:

We divide the first term of the above result by 'x' again to get the second term of the quotient.

⇒
`(-5x)/(x)=-5`

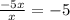
Now, we multiply '-5' to
`(x+4)`

⇒
`-5(x+4)=-5x-20`

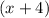
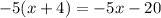
Now, we subtract
`-5x-20` from the result obtained at the last of step 1
`-5x-20`. This gives,

`-5x-20-(-5x-20)=-5x+5x-20+20=0`

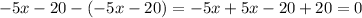
So, we stop division as we got a constant after subtraction. The constant is called the remainder and here the remainder is 0.

The quotient is our answer:
`3x-5`