Answer:
Domain : x ∈ ( ∞ , ∞ )
Range : f(x) ∈ ( 1 , ∞ )
A graph of f(x) is attached with this answer.
Explanation:
A theorem you must keep in mind while solving this question:
If domain of h(x) is ( ∞ , ∞ ) and domain of g(x) is also ( ∞ , ∞ ) then domain of f(x)=h(x)+g(x) will also be ( ∞ , ∞ ).
Here, assume h(x) = |x| and g(x) = cos(x). The domain of h(x) is ( ∞ , ∞ ) as no real value of x stops the function of modulus function. Same for g(x), domain of it is ( ∞ , ∞ ).
Therefore domain of f(x) is ( ∞ , ∞ ).
There is no perfect method to find range of a function. The only way to get the range is to analyse the function over its whole domain or analyse its graph. According to the graph attached the minimum value of the function is 1 at x = 0 and the maximum value is positive infinity. You can find this with some mathematical calculation which are as follows :
Let's first check the maximum value of f(x) : Maximum value of |x| is infinity when value of x tends to +∞ or -∞ but the value of cos(x) still oscillates between -1 and +1 , so on adding |x| and cos(x) when x → ∞ the resulting value will be ∞. Therefore the maximum value of f(x) will be ∞.
To find the minimum value of f(x), first check the behavior of f(x) in its domain (it is increasing or decreasing). For that open the modulus
f(x) = x + cos(x) ; x ≥ 0
= -x + cos(x) ; x < 0
f'(x) = 1 - sin(x) ; x > 0
= -1 - sin(x) ; x < 0
f'(x) = [ 1 - sin(x) ] ≥ 0 for all x > 0
= [ -1 - sin(x) ] ≤ 0 for all x < 0
from above calculations we conclude that f(x) is decreasing when x varies as ( - ∞ , 0 ) and value of f(x) varies as ( 1,+∞) (as you know f(0) = 1 ) whereas f(x) is increasing when x varies as ( 0 , +∞ ) and the value of f(x) varies as ( 1 , +∞ ). As you can see the value of f(x) approaches to minimum of 1 when x=0. Therefore minimum value of f(x) is 1.
(NOTE :
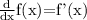
If the first derivative of a function is positive then function value is increasing and if first derivative of the function is negative then function is decreasing )