Answer:
1) 57 revolutions.
2) 4.52 m
3) 1531.2 m
Step-by-step explanation:
Question 1:
Given:
Initial velocity,
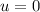
Final velocity,
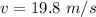
Time,
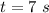
Acceleration,
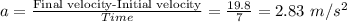
Now, displacement of the tire is given as:
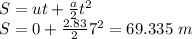
Displacement of tire in 1 revolution is equal to its circumference.
Therefore, displacement in 1 revolution =
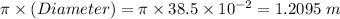
Now, number of revolutions is given as:
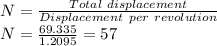
Therefore, the number of revolutions are 57.
Question 2:
Given:
Radius of the wheel is,
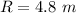
Angle of rotation is,
 °
°
Converting degree to radians, we get:
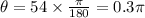
Now, path length is given as:
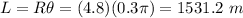
Therefore, the path length of a point on the wheel is 4.52 m
Question 3:
Radius of the wheel is,
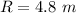
Angle of rotation is,
 radians
radians
Now, path length is given as:
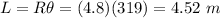
Therefore, the path length of a point on the wheel is 1531.2 m.